A journey through the Pythagorean table
The sun was setting on the horizon. It was a late afternoon on one of those days still under the old time, meaning an hour ahead of where we are now. Despite the time being ahead, I will not talk about the future. On the contrary, I will speak of two recent and distant pasts.
In the recent past, while traveling on a highway, I was suddenly struck by a beam of light (fortunately, not a lightning bolt) that made me reflect on the multiplication table and transported me to a distant past. Suddenly, as if in a leap through time, I found myself in the 6th century BC, on an island in ancient Greece, face to face with Pythagoras. Who does not know the well-known rhyme that describes his famous theorem?
"On the way to Syracuse, Pythagoras told his grandchildren: The square of the hypotenuse is equal to the sum of the squares of the other two sides."
Although the theorem is fascinating, it is irrelevant to today’s topic. Beyond the theorem and many other significant contributions, Pythagoras developed a table—now known as the Pythagorean Table (Table 1). This table contains all multiplications, making learning the multiplication table without memorization easier.
For example, we find the sequence 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 along the main diagonal. This sequence can be obtained by adding the first odd number (1) to the next odd number (3), and continuing this pattern along the diagonal using the rest of the sequence of odd natural numbers given by the set A = {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}. That is:
1 + 3 = 4,
4 + 5 = 9,
9 + 7 = 16, etc.
The same reasoning can be applied to all diagonals parallel to the main diagonal. All values are obtained by sequentially adding to the starting natural (odd) number the next number of the same class in the sequence.
Beyond being a mathematician and philosopher, Pythagoras also contributed to astronomy and music theory. He was also known as a numerologist, having established a relationship between planets and their “numerical vibration,” known as the harmony of the spheres. Given his extensive work, why not think beyond mathematics? Could Pythagoras have discovered hidden secrets within this table? Did he intentionally embed them in the structure he created?
When exploring this idea, patterns emerge - not immediately visible at first glance. Let’s look at some examples.
1. Recursive reduction
I performed the first multiplication mentally and quickly—after all, I was on the highway! I started with 8:
- 8 × 1 = 8
- 8 × 2 = 16 → (1 + 6 = 7)
- 8 × 3 = 24 → (2 + 4 = 6)
- 8 × 4 = 32 → (3 + 2 = 5)
- 8 × 5 = 40 → (4 + 0 = 4)
- 8 × 6 = 48 → (4 + 8 = 12 → 1 + 2 = 3)
- 8 × 7 = 56 → (5 + 6 = 11 → 1 + 1 = 2)
- 8 × 8 = 64 → (6 + 4 = 10 → 1 + 0 = 1)
- 8 × 9 = 72 → (7 + 2 = 9)
By considering only the result of the digit reduction, we identify an interesting sequence: 8, 7, 6, 5, 4, 3, 2, 1, (9).
With this in mind, it became imperative to write down all the multiplications. The result exceeded my expectations! I discovered that all rows behave similarly. When reduced to a single digit, the values from 1 to 9 follow different orders and do not repeat. However, the multiplications of 3 and 6 behave differently—making them exceptions to the rule. This exception, however, enhances the fascination, as 9 and 6 are multiples of 3.
In the multiplication tables of 3 and 6, we observe three repetitions of the sequences 3-6-9 (for 3) and 6-3-9 (for 6). Interestingly, 6 + 3 = 9.
2. The Sum of Each Row
The numbers in each row can be summed, and their total reduced to a single digit. Let’s take the row for 8 as an example:
8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 9 = 45 → 4 + 5 = 9
Since the values in each row do not repeat and are distributed between 1 and 9, the total is always the same: 9.
The only exception is found in the multiplication tables of 3 and 6, where the sum is 54. But 54 can also be reduced to 9 (5 + 4 = 9). Furthermore, 54 = 45 + 9.
It becomes increasingly evident that the number 9 holds a central role in the entire table.
3. The Unique Behavior of 9
Looking at the multiplication table of 9, we find that the sum of the digits of any product in that row always results in 9. This is an example of the digital root property of the number 9, which arises from the behavior of numbers in base 10.
Connecting this observation with the previous point, we see that 9 is the number that gathers all values together.
Pythagoras believed that numbers were not merely abstract concepts but the language of the universe. To the Pythagoreans, the number 9 represented completion and universal wisdom, often associated with perfection and spiritual fulfillment.
Could it also be a symbol of spiritual unification?
4. The Symmetry of the Table
The fascination with the Pythagorean Table continues. Despite the surprising results obtained, other patterns lead me to believe that there are still hidden mysteries within these multiplications.
Did Pythagoras intentionally encrypt a message within them?
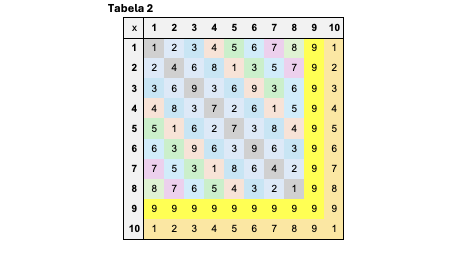
When we divide the table along the main diagonal, we notice that it is symmetrical. (Of course, this is not a groundbreaking discovery—we are simply recognizing the commutative property, meaning that 2 × 5 = 5 × 2, making the upper triangle identical to the lower one.)
However, if we look only at the upper triangle of Table 2, another curiosity emerges. While the diagonals do not display perfect symmetry, if we transform them into rows, we arrive at an astonishing conclusion:
The numerical sequence obtained in the diagonal is identical to the sequence in its corresponding column (Table 3).
This confirms the existence of a symmetrical pattern in the results along the diagonals. Additionally, we once again encounter the intriguing number 9, which appears whenever we add the row number and the column number where the diagonal is traced.
For example, from column 1 to row 8, we have:
1 + 8 = 9.
5. Finally, a Moment to Unwind…
We can also find geometric patterns within the table obtained after applying recursive reduction.
Take a look at Table 4.
Food for Thought:
What is the reason behind the numerical distribution (1 to 9) in the results, and how is it possible that it never repeats? [Table 2]
What explains the mirror-like behavior of the diagonals? [Table 3]
Why does so much of this reduce to the number 9?
In numerology, 9 is considered the number of completion, associated with cycles, life purpose, goals, and new beginnings. Because it marks the end of cycles, it is seen as a number of learning and renewal, closely linked to spiritual wisdom.
What message could be hidden here? What secrets might Pythagoras have concealed in the multiplication table?
Talk to us: pxp.cminho@gmail.com
Column published in Correio do Minho on December 12, 2024.
Comments
Post a Comment